Mint minden elméletnek, a játékelméletnek is megvannak a maga egyszerűsítő feltevései. Ilyen a játékosok racionalitása, azaz, hogy rendes homo oeconomicushoz illően maximalizálják a kifizetésüket. Így egy nonkooperatív játékben a játék kimenetelét a Nash-egyensúly határozza meg, mely a különböző játékosok egymás stratégiáira adott legjobb válaszaiból áll. Hogyan válasszuk meg a nyerő stratégiákat, ha az ellenfél nem racionális: konkrétan, ha már hozott irracionális döntéseket?
Alexandru Baltag az LGS7 konferencián tartott előadásában a tudás - racionalitás - vélemény-reformálás (belief-revision) témát járta körbe. Elkezdünk játszani egy játékot: a szabályok ismertek és feltételezhetjük, hogy az ellenfél képes jó döntéseket hozni. Vegyük például az alábbi játékot. Két játékosunk van, akik felváltva léphetnek. Ádám kezd, majd Éva következik és így tovább. A játéknak négyféle kimenetele lehet.
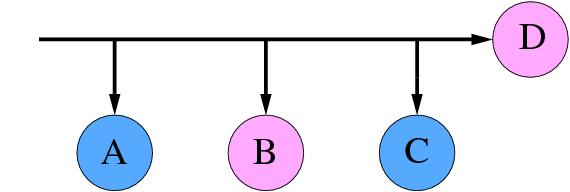
Ádám preferenciái: C > A > D > B
Éva preferenciái: D > B > A > C
Ay ilyen típusú játékokat Selten óta fordított indukcióval oldjuk meg:
- Először megnézzük, mi történik az utolsó döntés során. Mivel Ádám szerint C > D, ezért "C"-t választja, nem "folytatja" a játékot. Ezzel lényegében letörölhetjük a "D" kimenetelt.
- Most Éva dönt. Tudván, hogy ha a folytatás mellett dönt, Ádám ki fog szállni ("C" kimenetel), a "B" és a "C" kimenetelek közül kell választania. Mivel szerinte B > C, inkább kiszáll "B"-nél.
- Végül eljutunk az első döntési ponthoz; itt az előbbiekhez hasonló megfontolásból Ádám a kiszállás, azaz "A" mellett dönt, hiszen A > B.
Ez a megoldás ugyanakkor tartalmaz egy logikai ellentmondást. Baltag előadása pontosan erre az inkonzisztenciára kívánta felhívni a figyelmet: Ha ugyanis a játékosok racionálisak, akkor a második döntési ponthoz sose fogunk eljutni. Magyarul ha mágis eljutottunk ide, akkor valami nagyon szokatlan dolog történt, valami, amit az elméletünk nem tud megmagyarázni. Úgy tűnik Ádám hibázott, Éva behúzza "B"-t. Ádám lépése ugyanakkor össze is zavarhatja Évát: ha Ádám egyszerűen rosszul játszik, hibázhat megint és az Éva számára ideális "D" kimenetel is egy elérhető alternatívának tűnik. Ha tehát Ádám irracionális, érdemes folytatni a játékot. Ezzel Ádámnak "C" és "D" közül kell választania - természetesen kedvencét "C"-t választja. Ezzel viszont jobb eredményt ér el, mintha az első lépésnél kiszállt volna. Tehát mégis racionális volt. Ha azonban racionális, akkor már a második csomópontig sem lett volna szabad eljutnia, mert utána igen-igen pórul jár.
Hm... nem tudom, mennyire világos a példa. Valami olyasmiről van szó, hogy egy látványos hibával elhitethetjük az ellenféllel, hogy az egyensúlyinál lényegesen kedvezőbb feltételekkel zárhatja a játékot, s ha sikerül összezavarnia, a végén mi járhatunk jól. Nem tudom ilyesmit szokás-e a sakkban alkalmazni, de honfoglaló őseink menekülő harcmodora valami ilyesminek fogható fel.
