Alakul a Dallas folytatásának stábja, hiszen némi kéretés -és egy vaskosabb ajánlat- árán Larry Hagman is csatlakozott a visszatérő színészekhez. Hagman így jóval magasabb gázsiért fog dolgozni - milyen ügyes, mondhatnánk, de vajon mennyiben tudható be mindez a jó taktikának?

Legyen szó fizetésről, autó-, vagy lakásvásárlásról, mi is gyakran kerülünk alkuhelyzetbe. Hogyan alkudjunk?

Nem vagyok kőkemény Dallas rajongó,  - szerintem a kezemen meg tudom számolni, hány epizódot láttam, - de ha valamiért érdemes lenne nézni a sorozatot az éppen Jockey karaktere és persze ahogy azt Hagman alakította. Egy gyors közvéleménykutatás a közvetlen környezetemben azt mutatja, hogy ezzel nem vagyok egyedül, s ha általánosíthatunk világos, hogy Hagman egyszerűen többet ér a sorozatnak, mint a több színész (akiknek nevét sem tudom) együttvéve. Így az alku nem annyira Hagman jó taktikájának, mint népszerűségének köszönhető.

Az alku - nem túl meglepő módon - a kooperatív játékelmélet egyik fontos területe. Nézzük meg, röviden, hogy a játékelmélet hogyan modellezi a problémát és milyen megoldásokat kínál.

Kooperatív játékokról van szó, tehát a két fél együttműködik. Pontosabban megengedjük azt is, hogy ne működjenek együtt, sőt: az együttműködés hasznát ehhez (a lenti ábrán (u*,v*)) viszonyítjuk. Az egyszerűség kedvéért feltételezzük, hogy az egyet nem értési pontban a felek hasznossága 0. Igen, hasznosságról beszélünk, ez egy picit általánosabb, mintha kifizetést mondanánk.

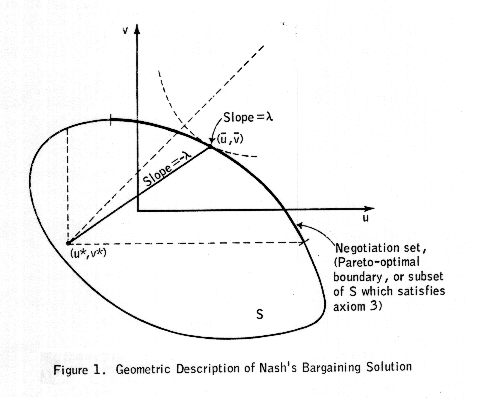A fenti ábrán jól látható az S halmaz, ami az alku lehetséges kimeneteleit tartalmazza. Erősen valószínű, hogy az eredmény a halmaznam nem valamely belső pontja lesz, hanem valamely, a Pareto-határon található pont. Ezekre teljesül ugyanis, hogy egyik fél sem növelheti hasznát a másik fél hasznosságának csökkentése nélkül. Hangsúlyozom, hogy itt hasznosságokról van szó. Így ha az egyik fél hasznosságának növekedése irígységet kelt bennem, akkor a hasznosságom csökken és máris a Pareto-határon vagyunk. Hagman esetében a tárgyalásnak két fő eleme lehetett: a visszatérés ára és "mértéke" azaz, hogy milyen súlyú szerepet kap. Általában feltételezhetjük, hogy az ábrán láthatóhoz hasonló "krumpli" adja a megállapodások lehetséges halmazát -ebben az (u*,v*) ponttól délre, vagy nyugatra levő pontok nem igazán érdekesek. Kérdés, hogy melyik pontban állapodnak meg a felek.

Mielőtt a megoldásra rátérnénk, tisztázzuk, mit is jelent a "megoldás." A megoldás meghatározásánál feltételezzük, hogy a felek tökéletesen informáltak és tökéletesen racionálisak. Ekkor a megoldásnak két értelmezése is van. Az egyik, a kooperatív megközelítés lefektet bizonyos axiómákat és a költésgmegosztás esetéhez hasonlóan ezek egyértelműen meghatározzák, hogy hogyan kell megoldanunk egy tetszőleges alkujátékot, azaz az axiómák a megoldó szabályt rögzítik. Ugyanakkor Nash igazolta, hogy ugyanez a megoldás előáll egy megfelelő, természetes módon definiált nonkooperatív játék egyensúlyaként is. Magyarul ha a felek inkább az alkudozást választják, akkor is ugyanerre fognak jutni, így sokkal egyszerűbb lenne felrajzolni a krumplit, megkeresni a megoldást és ezzel rengeteg időt, stb megtakaríthatnánk (bár ezzel egy jó mulatságról is le kellene mondanunk).

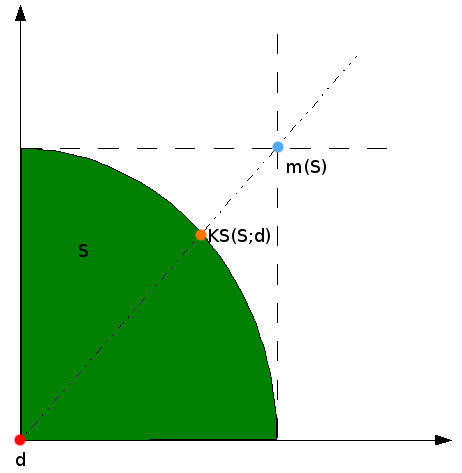Mi a megoldás? Megoldás több is van: ennek egyik oka, hogy változhat mit várunk el a megoldástól, másrészt ennek megfelelően egy kicsit más nonkooperatív játéknak máris kicsit más lesz az egyensúlya. A legismertebb a Nash alkumegoldás, ami a két (relatív) hasznosság szorzatát maximalizálja. A másik, a Kalai-Smorodinsky megoldás (balra) pedig a diktátor-hasznosságok (azaz a másik fél figyelembe vétele nélküli legmagasabb hasznosságok) arányát adó hasznosság-pár. Ezek csak a legritkább esetben esnek egybe, miközben van aki az egyikre, van, aki a másikra esküszik. A Nash-féle megoldás két fő axiómája kimondja, hogy az eredményt ne befolyásolja, ha elhagyunk pár elvetett megállapodási lehetőséget. Ezzel szemben a KS megoldásnál a diktátor-javaslatok szinte sose kerülnek elfogadásra, miközben komoly szerepük van a megoldás meghatározásában. Mindkettőre igaz, hogy az eredmény nem függ a hasznosság mértékegységben, azaz független attól, hogy egy pénzben számontartott hasznosság esetén milyen pénznemmel számolunk. Ez már nem teljesül az egalitáriánus megoldás esetén, ami mindkét félnek ugyanannyit ad. Nem mindegy ugyanis, hogy az ugyanannyi dollárban, euróban, vagy éppen forintban kerül kifizetésre.

Egyszer megkerestek egy kérdéssel, hogy segítsek egy munkaadó és a munkavállalók közötti tárgyalásokban - az egyik félnek. Sajnos a rövid válasz az, hogy ismerve a játék részleteit meg tudom mondani, hogy mi lesz a tárgyalás eredménye, de ezen változtatni nem tudunk. Ezt az egyes felek alkuképessége határozza meg. A hosszú válasz ennél összetettebb, hiszen a gyakorlatban több általánosan feltett tulajdonság nem teljesül. Amikor egy használt autóra alkuszunk, nem tudhatjuk a kocsi valódi állapotát - szemben a tulajjal, aki talán épp ezért kínálja eladásra. A vásárló ugyanígy nem biztos, hogy feltárja a tulaj előtt, hogy pont itt és pont ilyen lakást szeretne és tulajdonképpen évek óta keresve ez az első lakás, ami megfelel. Ezen információk hiányában a hasznossági görbék, illetve a megegyezés hiányában járó hasznosságok teljesen máshogy festenek és általánosan igaz, hogy jobb eredmény érhetünk el, ha az alku számunkra kisebb jelentőségű és ha nem születik megegyezés, tulajdonképpen az is jó.

Pamela, vagy Bobby nélkül lehet Dallas 2-t forgatni, de mindenki számára világos, hogy a Dallas-remake sikere szempontjából Jockey kulcsfontosságú. Bár a filmet készítő TNT bepróbálkozott azzal az ötlettel is, hogy Jockey csak az eredeti Dallasból vett jelenetekben legyen látható, végül sikerült megegyezniük. Úgy gondolom, hogy Hagman megérdemli a magasabb gázsit, bár az alkudozásban talán egyetlen érdeme, hogy hajlandó volt várni.

Hivatkozások

Kalai, E., and M. Smorodinsky (1975):  Other Solutions to Nash’s Bargaining
Problem, Econometrica, 43, 513–518.

Nash, J.F., (1950): The Bargaining Problem. Econometrica, 18, 155-162.

Kiegészítés!

Február 14.-én reggel 9:50-10:50-ig Bram Driessen "The Kalai-Smorodinsky bargaining solution with loss aversion" címmel tart előadást a Corvinus egyetemen. További info.