A KRTK "Economics with Policy" előadássorozatának következő alkalmával szeptember 11-én csütörtökön du. 2 órakor a Budaörsi út 45. VIII/807 szeminárium-teremben Tim Roughgarden a Stanford Egyetem associate professzora tart előadást Approximately Optimal Mechanism Design: Motivation, Examples, and Lessons Learned címmel. Tim amellett, hogy egy híresen szimpatikus kutató, kiváló, szórakoztató előadó, fiatal kora ellenére olyan eredményeket mutathat fel, amikre akárki büszke lehetne. Bár témavezetője a magyar Tardos Éva, a Cornell professzora, ez az első alkalom, hogy Timet hazánkban láthatjuk vendégül.
A Közgazdasági és Regionális Tudományok Kutatóközpontjának új szeminárium-sorozatába nemzetközileg elismert külföldi kutatókat hívunk meg. Jövő csütörtökön a vendég Tim Roughgarden a Stanfordról. (Aki szeretne Timmel előadása után szakmai kérdésekről beszélgetni, előzetesen keressen meg igényével és megpróbálunk erre lehetőséget teremteni)
Tim doktori fokozatát 2002-ben a Cornellen szerezte Tardos Éva témavezetése mellett.Több tucat cikket, könyvfejezetet jegyez algoritmikus játékelmélet, aukciók, mechanizmustervezés, forgalomirányítás témakörökben; munkáját díjazta az ACM, a Mathematical Programming Society, az INFORMS operációkutatási társaság. A GAMES 2008 játékelméleti világkongresszuson ő tartotta a fiatal tehetségeknek fenntartott Shapley-lecture-t, 2012-ben pedig az algoritmikus játékelmélet alapjainak lefektetéséért megosztva megkapta a Gödel díjat.
Kezdetben forgalomirányítás érdekelte, azon belül is, hogy mi a forgalomban részt vevő autósok önző viselkedésének hatása a társadalmi jólétre. Vegyünk egy egyszerű példát. Egy városon szeretnénk átjutni (s-ből t-be), s az átjutás kétféle útvonalon lehetséges. Van egy elkerülő út, ami ugyan hosszú (1 óra), viszont széles, így az utazási idő nem függ a forgalomtól, s van egy városi út is, ahol a dugók miatt az utazási idő a forgalommal arányos: mindez felírható az alábbi ún. Pigou gráffal.
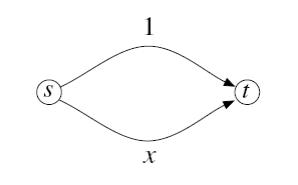
Ha összesen egységnyi forgalmat kell átvezetni, nem nehéz belátni, hogy társadalmilag az lenne a legjobb, hogy ha a társaság fele-fele arányban oszlana meg a két útvonal között, így 0,5x1+0,5x0,5=3/4 lenne az összes utazási idő. Ez azonban úgy adódik össze, hogy a felső, elkerülő utat választó autósok 1 órát utaznak, míg a városon keresztül utazók x=0,5 órát. Így a felső utat választó autósnak önző érdeke, hogy inkább az alsó, gyorsabb utat válassza figyelmen kívül hagyva döntésének külső hatását, externáliáját, hiszen ezzel a többi alsó utat választó autós utazási idejét is megnöveli. Mivel ez a gondolkodás a többi felső utat választó autósra is igaz, végül Nash egyensúlyban mind az alsó utat választják, s így az összes/átlagos utazási idő 1x1=1. Az individualizmus, az anarchia ára (price of anarchy) itt 33%, hiszen ennyivel nőtt meg az utazási idő. Roughgarden igazolta, hogy lineáris késlekedési függvények esetén az anarchia ára ennél nem lesz magasabb. Ha általános nemcsökkenő késedelmi függvényeket nézünk, akkor is igaz, hogy nem lesz nagyobb az összes utazási idő, mintha kétszer annyi autóst küldenénk át a városon, de optimális bontásban. Egy másik cikkben azt is megállapítja, hogy ezek a korlátok nem függenek a hálózat topológiájától, így a legrosszabb eset előáll egy (általánosított) Pigou gráfon is.
Ezek az eredmények azt sejtetik, hogy megoldást csak az utak bővítése, további utak építése hozhat. Ez általában igaz is, de esetenként az új utak építése még káros is lehet. Az alábbi ábrán azt látjuk, hogy s-ből t-b két úton is el lehet jutni, v-n, illetve w-n keresztül. Mivel a két út szimmetrikus, az autósok fele-fele arányban oszlanak meg, az utazási idő 2x0,5x(0,5+1)=1,5.
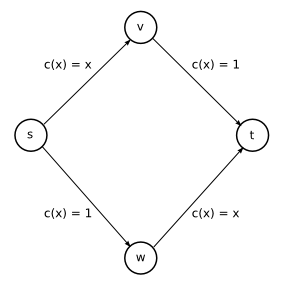
Mi történik akkor, ha a v és w pontok között egy nagyon gyors kapcsolatot építünk?
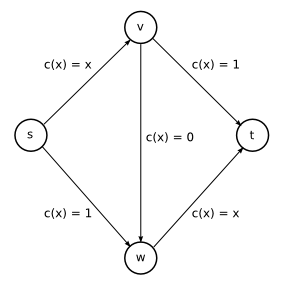
Itt már megjelenik ugyanaz az okoskodás, mint a Pigou gráfban, egyensúlyban mindenki az s-v-w-t útvonalon autózik és a teljes utazási idő 2 lesz, magyarul a plusz út ront a hatékonyságon. Felesleges, sőt káros út bonyolultabb hálózatokban is felbukkanhat, azonban Roughgarden kutatásai szerint ezen élek megtalálása NP-teljes feladat, ami azt jelenti, hogy egy nagyobb térképen gyakorlatilag lehetetlen, s a közelítő algoritmusok segítségével megtisztított úthálózat még mindig akár n/2-szer nagyobb utazási időt igényelnek (n a csúcsok száma), mint az optimális esetben, magyarul nem sokat érnek.
Miután idáig eljutottunk, elárulhatjuk, hogy Tim ezúttal nem forgalomirányítási kérdésekről fog beszélni, hanem olyan mechanizmuskoról, pl. aukciók esetében, ahol az optimális megoldás megtalálása hasonlóan nempolinomiális komplexitású, azaz szinte lehetetlen megtalálni. Hogy egy ilyen példát is mutassunk korábbi munkáiból (egy kicsit más sztorival), vegyük az állami támogatások elosztásának esetét. Mindenki (mondjuk cégek) szeretnének minél több pénzt kapni. Mondjuk egy fagyizó pár százezerből tud venni egy jobb fagyigépet, ugyanakkor annak, aki szállodát szeretne építeni ez a pénz értéktelen. Ha a fagyisnak adunk százmilliót, vehet több fagyigépet is, de nem várhatunk robbanásszerű növekedést a befektetés megtérülésében. Ugyanakkor a szállodás egy bizonyos összeg felett fel tudja építeni a szállodát és (tegyük fel) ekkor már sokkal magasabb hozammal számolhatunk. Nem is az a lényeg, hogy a nagyobb befektetés többet hoz, hanem hogy a különböző vállalkozásoknak adott támogatások megtérülési görbéje nem azonos, más-más összeget tudnak jól hasznosítani. A kérdés az, hogy ezek tükrében hogyan osszuk el a támogatást. A leírt sztori persze nem más, mint egy aukció, ahol a megszerezhető tárgyakért (=támogatás) licitálnak (=megtérülést ígérnek) a cégek, de a megtérülés erősen függ attól, hogy hány terméket kap a licitáló. Sajnos ez is egy nehéz feladat, amire csak közelítő megoldások léteznek. Kb ilyesmiről lesz szó a csütörtöki előadásban.
A szerző köszöni Sziklai Balázs segítségét.
